The study of graphs consisting of nodes connected by edges representing some pairwise relation are of interest to security experts who wish to model complex computer or server networks. My paper describes several applications of graph theoretic results in cybersecurity, one of which is introduced here.
The healthcare industry is a frequent target of cyberattacks due to overworked hospital staff, a problem only exacerbated as a result of Covid 19. Confidential patient data can be sold or ransomed for a lot of money, and hospitals often rely on outdated technology to keep information secure. The concept of a dominating set may be utilized when a lack of sufficient resources makes it impossible to guard every component of a system.
We might model defenders as mobile guards defending a network, where a guard on vertex v can protect against an attack on any server adjacent to v by an edge. This set of vertices is known as the neighborhood of v, denoted N(v). If every vertex is protected in such a way by at least one guard, the network is said to be dominated. The problem of determining the size of a minimum dominating set is an exact solution for efficiently defending networks against worm propagation.[1]
Consider the small grid below. Guards located at vertices u, w, and y would dominate the graph, but so would two guards located at x and w. Since no vertex is adjacent to all other vertices, a dominating set of size 1 cannot exist, and hence the minimum domination number of the graph is 2.
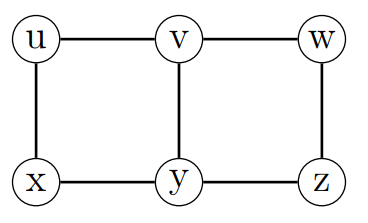
A dominating set S is secure if exchanging a vertex outside of the dominating set for its neighbour in S results in a new dominating set. In our application, the network remains dominated even after a mobile guard were to move from his node to a neighboring node. In figure 1, the set {u, w, y} satisfies the secure dominating set condition but {x, w} does not: if vertex z were to be attacked, the guard on w would have to move, leaving v uncovered.
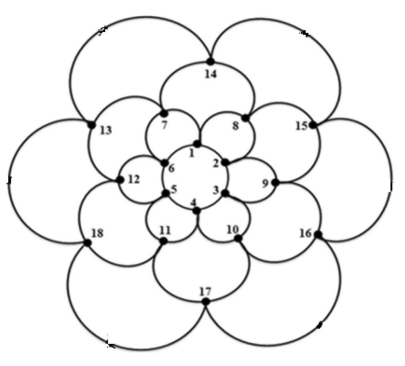
Although determining the minimum size of a dominating or secure dominating set is NP-complete, exact constructions can be found in linear time for certain families of graphs. One such family is bloom graphs (above), whose symmetry and structure makes them appealing for large-scale parallel computer networks. It was shown in [1] that if Bm,n is a bloom graph with m ‘layers’ of n ‘petals’ each, the smallest possible secure dominating set has size n(ceiling(m/2)).
With a secure dominating set in place, safeguarding the nodes of the network and monitoring for any potential deficiencies becomes a significantly easier task.
References:
- [1] Angel, D. (2022). Application of graph domination to defend medical information networks against cyber threats. Journal of Ambient Intelligence and Humanized Computing. 10.1007/s12652-022-03730-2.
- [2] Lesniak, L., Chartrand, G., and Zhang, P. (2015). Graphs & Digraphs. United States: CRC Press.
- [3] Webb, J., Docemmilli, F., and Bonin, M. (2015). Graph Theory Applications in Network Security. SSRN Electronic Journal. 10.2139/ssrn.2765453.

Interesting post I realize that graph theory was used in cyber security but I didn’t know how it would be implemented and used. I liked how you described a computational problem that a lot of CPSC students are familiar with and showed its use, it seems like there are ‘hard’ problems that aid in cyber security because of their hardness and some that prevent systems being secure like what you mentioned. I didn’t know that some types of graphs are easy to solve for the minimum dominating set which was interesting. Great read overall!
I think the images use and the explanation of comparing it to mobile guards defending a network was a great way to explain how useful graph theory can be especially with the visuals provided making it easy to understand. It also makes sense now why bloom graphs would be so appealing for large scale computer networks.
Great post! Its an interesting application of graph theory. I’ve seen graph theory come up several times in other applications such as Neo4J (a graphical database). You did an excellent job at explaining the application of graph theory and your analogies were spot on.
Great read! It’s very interesting seeing how you compared a theoretical topic learned in Computer Science to an actual real life issue. Additionally, even though graph theory spans back to the 18th century, it is still finding uses for modern day applications. It really makes you think how current theoretical mathematics may be applied to future problems we are unaware of right now.
A really interesting post, and one that was totally new to me. I’m not going to lie, as a dumb art student that’s taking this class most mathematical terms and concepts tend to fly over my head, so that fact that I understood both the underlying background and the arguments that you were presenting is a testament both to your project and your writing skills.
I fail to see the relevance to cybersecurity, but in terms of regular security this makes a lot of sense! I had no idea that “graph theory” was so relevant.
It’s interesting to see graph theory applied to help improve cybersecurity especially for the healthcare industry which desperately needs it. Hopefully we’ll be seeing companies using this method or any other method to help enforce their systems, but considering how negligent they are shown by their outdated systems it makes me skeptical that we’ll be seeing change. Nice post!
Interesting post. It is a good idea to use graph theory to describe the application of network security. It is also good for you to integrate the concept of dominating set into practical application. In order to avoid becoming the target of network attacks, it is necessary to update the technology to protect network security in real-time. The dominant network structure seems to be a strong protection system. Because in the grid, the guard on each vertex can prevent the attack of adjacent servers. If the targets vulnerable to network attacks have secure control devices, they can protect their network data, find potential defects and prevent them.
I never realized that theoretical math concepts were so applied in this field. Interesting to see abstract ideas come to light and be useful in the real world. People always tend to think of statistics as a useful branch of math, but I guess there are many more as well.