Walkthrough : https://youtu.be/7MXVV858loU
Code Example Link: https://github.com/HaydenMcNally/ISEC-611
Introduction to Garbled Circuits (History and Overview)
Garbled circuit is a computational technique which Andrew Yao introduced in an oral presentation in 1986, and the first written document was authored by Goldreich, Micali, and Widgerson in 1987. The term “garbled circuit” was coined by Beaver, Micali, and Rogaway in 1990. The primary goal was to enable two parties to jointly compute a function using their private inputs while ensuring that neither party gains access to the other’s input. This protocol is particularly useful in scenarios where trust is limited, and secure computation is required without reliance on a trusted third party.
Yao’s protocol was first demonstrated in the Millionaires’ Problem, where two individuals determine who is wealthier without disclosing their actual wealth. The problem discusses two millionaires, Alice and Bob, who are interested in knowing which of them is richer without revealing their actual wealth. This problem is analogous to a more general problem where there are two numbers a and b, and the goal is to determine whether the inequality a≥b is true or false without revealing the actual values of a and b was the first example of secure computation [3].
The concept extends beyond this problem, enabling secure computations in various applications, such as privacy-preserving data mining, secure voting, confidential transactions, and privacy-focused AI computations.
What is Garbled Circuits?
Garbled circuits are a cryptographic protocol that allows two parties to securely compute a function over their private inputs without needing a trusted third party. This is achieved by representing the function as a Boolean circuit and using Oblivious Transfer to ensure input privacy [2].
In private data computation, one of the objectives is to compute data without the other party knowing the details of the data set.
Privacy preserving data mining (PPDM) deals with protecting the privacy of individual data or sensitive knowledge without sacrificing the utility of the data. People have become aware of the privacy intrusions on their personal data and are very reluctant to share their sensitive information [1]. Also, some regulations on how personal data is handled requires some computational techniques to protect the privacy of individual/sensitive data.
Garbled circuit is a technique used in a multi-party Privacy Preserving Data Minning (PPDM).
At its core, the Garbled Circuit protocol involves representing a function as a Boolean circuit, where each logical gate is encrypted in such a way that only the correct sequence of inputs can reveal the output. The process consists of three main phases:
- Circuit Garbling – One party (the garbler) encrypts the circuit using randomly assigned encryption keys for each input.
- Oblivious Transfer – The evaluator (the second party) receives encrypted input values corresponding to their private data without revealing their actual input to the garbler.
- Circuit Evaluation – The evaluator decrypts the circuit and computes the output without learning any information about the garbler’s inputs.
Uses of Garbled Circuits
- Garbled circuits have applications in:
- Secure Data Analysis – Enabling privacy-preserving computations on sensitive data.
- Electronic Voting Systems – Ensuring voter anonymity and election integrity.
- Blockchain – Enhancing smart contract privacy and security.
- Confidential Transactions – Protecting financial data in secure payments.
How Does Garbled Circuits Work?
Suppose that there are two parties, Alice and Bob, who want to compute some function f (alice_inputs, bob_inputs), which takes inputs from both parties. Alice and Bob both want to learn the result of computing f, but Alice does not want Bob to learn her inputs, and Bob does not want Alice to learn his inputs. Ideally, they would both learn nothing except for just the output of function f [5].
Garbled circuits enable the two parties, Alice and Bob, to compute the function while keeping their inputs private from each other.
- Alice performs a special procedure (“garbling”) to encrypt a circuit (meaning, a set of AND, OR… gates) which evaluates the function f. She passes along inputs, also encrypted in a way that’s compatible with the encrypted circuit, to Bob.
- Bob uses a technique called “1-of-2 oblivious transfer” to learn the encrypted form of his own inputs, without letting Alice know which inputs he obtained.
- Bob runs the encrypted circuit on the encrypted data and gets the answer and passes it along to Alice.[5]
Classical Yao’s garbled circuits.
- Alice creates the truth table based on the circuit.
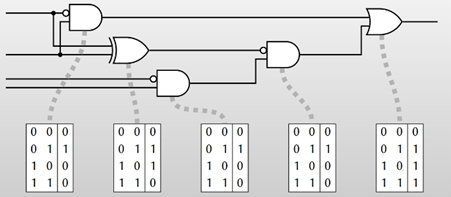
2. Alice assigns two randomly generated strings, known as labels, to each wire in the circuit: one for Boolean semantic 0 and one for 1. The label is typically k bits in length, where k is the security parameter, and is usually set to 128. Alice then proceeds to all the gates in the circuit and replaces 0 and 1 in the truth tables with the corresponding labels.
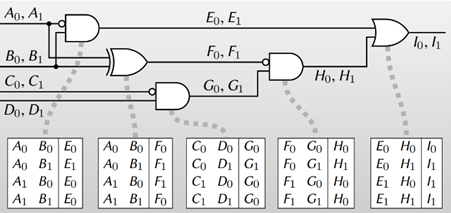
3. Alice then encrypts the output entry of the truth table using the corresponding two input labels. This encrypted table is the garbled table, which can be decrypted only if one possesses the correct two input labels. In the table below, double-key symmetric encryption is employed, and (A0, B0) represents the secret key, while E0 denotes the value to be encrypted.
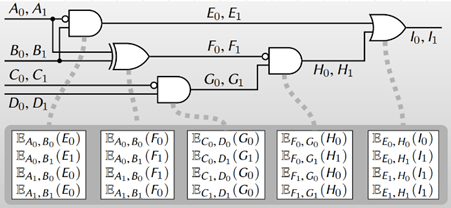
4. Alice then randomly permutes the table such that the output value cannot be determined from the row. The protocol’s name, garbled, is derived from this random permutation.
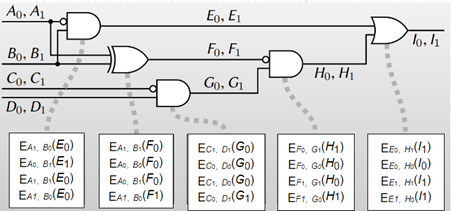
5. Alice sends Bob the computed garbled tables for all gates in the circuit. Bob needs input labels to open the garbled tables. Thus, Alice chooses the labels corresponding to her input and sends them to Bob. Let’s say A and C wires are Alice’s inputs, and B and D wires are bob’s inputs. For example, if Alice’s input is 10 (A1, C0), then she sends A1 and C0 to bob (Fig 4.). Bob will not learn anything about Alice’s input since Alice randomly generates the labels that look like random strings to Bob. Bob needs the labels corresponding to his input as well. He receives his labels through oblivious transfers for each bit of his input. For example, if Bob’s input is 01(B0, D1), Bob first asks for b=0 between Alice’s labels B0 and B1. Through a 1-out-of-2 oblivious transfer, he receives B0 and gets D1 similarly. After the oblivious transfers, Alice will not learn anything about Bob’s input, and Bob will not learn anything about the other labels.
6. After the data transfer, Bob has the garbled tables and the input labels. He goes through all gates one by one and tries to decrypt the rows in their garbled tables. He can open one row (red row in Fig 6.) for each table.
7. After the evaluation, Bob obtains the output label (I0 in Fig6.), and Alice knows its mapping to Boolean value since she has both labels (I0, I1). Alice can share her information with Bob, or Bob can reveal the output to Alice so that one or both learn the output. [4]
Real-World Example (Notable Applications)
Garbled circuits have seen significant real-world applications, demonstrating their relevance in modern cryptography and secure computation. Some key areas include:
- Secure Data Analysis: Organizations can analyse encrypted datasets collaboratively without exposing individual records, ensuring compliance with data protection regulations.
- Electronic Voting Systems: Garbled circuits facilitate secure and anonymous voting, preventing tampering while ensuring privacy.
- Blockchain and Smart Contracts: Secure multi-party computations allow private transactions and decentralized finance (DeFi) operations without revealing transactional data.
- Confidential Transactions: Financial institutions leverage garbled circuits for privacy-preserving banking and fraud detection mechanisms.
- AI and Machine Learning: Privacy-preserving AI models use garbled circuits to train models on sensitive data without exposing the original inputs.
Addressing Vulnerabilities in Garbled Circuits
While garbled circuits are secure at the protocol level, implementations remain vulnerable to certain attacks. A notable concern is side-channel attacks, where attackers exploit the computational behaviour of the encryption process to infer secret inputs. Recent research has highlighted vulnerabilities in AES-based garbling, where secret-dependent execution sequences leak information. Addressing such issues requires:
- Use of Constant-Time Implementations: Ensuring encryption and decryption operations are independent of secret values mitigates timing attacks.
- Randomization Techniques: Introducing noise in circuit evaluation can obscure execution patterns and protect against side-channel exploits.
- Efficient Oblivious Transfer Enhancements: Strengthening the OT process prevents input leakage and ensures secure key exchanges.
Further research is needed to explore post-quantum secure garbled circuits that can resist quantum computing threats.
Conclusion
Garbled circuits represent a powerful cryptographic tool for secure two-party computations. Their applications in secure data analysis, voting, and blockchain demonstrate their relevance. While vulnerabilities exist, techniques such as constant-time execution and randomized encryption mitigate risks. Our project will provide theoretical insights and a practical demonstration, bridging the gap between research and real-world implementation.
References
- https://ieeexplore.ieee.org/document/6394662 authors of the paper Majid Bashir Malik, M. Asger Ghazi and Rashid Ali.
- https://en.wikipedia.org/wiki/Garbled_circuit#:~:text=Garbled%20circuit%20is%20a%20cryptographic,described%20as%20a%20Boolean%20circuit.
- https://encyclopedia.pub/entry/34557
- https://medium.com/zkpass/yaos-classical-garbled-circuits-4cbdbadf288e
Discussion Questions
1: Why do the point values added to the wire values in the code not leak any information?
2. How does Oblivious Transfer enhance the security of Garbled Circuits?
3. What are the key differences between Garbled Circuits and Homomorphic Encryption?
4. Are there any discovered vulnerabilities in the garbled circuit computational protocol?

