Walkthrough of the Teaching Aide: Shamir Secret Sharing
“Welcome! Today, we will dive into Shamir’s Secret Sharing”
Understanding cryptographic techniques is crucial for maintaining secure and reliable systems. Through this teaching aide, you will gain insights into Shamir’s Secret Sharing, a powerful method for dividing a secret into multiple parts (shares) that can only be reconstructed when enough shares are combined.
What You Will Learn
We will cover:
- Explaining Shamir Algorithm: A cryptographic technique that divides a secret into multiple parts (shares) such that the original secret can only be reconstructed when enough shares are combined.
- Lagrange Interpolation Formula: A key mathematical concept used in Shamir’s Secret Sharing to reconstruct the original secret from the shares.
We will also dive into real-world examples, like how companies such as Vault use Shamir’s Secret Sharing to protect root keys and how it is applied in IoT data storage to keep information private and accessible. Throughout our presentation, we will explore these examples to see how Shamir’s Secret Sharing works in practice and its real-world benefits.
Why This Topic Matters
Cryptographic techniques like Shamir’s Secret Sharing form the backbone of secure data management, allowing sensitive information to be protected even if some parts of it are compromised. This method provides robust security against data breaches and unauthorized access.
For example, in the case of Vault, the root key is split among multiple users, ensuring that no single user holds the entire key. This adds an extra layer of security by requiring a threshold of shares to trigger the unseal process. Our aide thoroughly explores these real-world applications, detailing how they ensure data integrity and prevent unauthorized access.
Why this works?
One of the fundamental mathematical properties used in Shamir’s secret sharing is the fact that it takes k points to define a polynomial of degree k – 1.
For example:
Only one line can be drawn between two points, & only one parabola crosses through the same three points. Only one cubic curve passes through the same four points, but an infinite number of lines can be drawn through a single point.
Engaging Presentation Format
We have designed this teaching aide to be interactive and engaging. It includes detailed slides and real-world case studies that show how Shamir’s Secret Sharing is applied. Plus, we have added visuals to break down complex ideas, making them easier to understand.
Engagement Activity
To deepen your understanding, we have done an implementation of Shamir’s Secret Sharing in Python. Feel free to download the code from the repository & run it yourself. The code is heavily commented explaining the logic.
Link – https://github.com/OscarConstantino/Shamir_share_secret_OACM
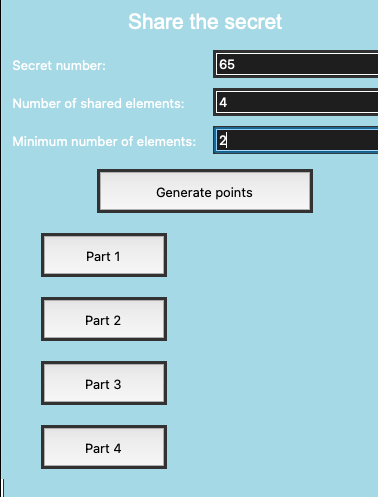

Objective of the implementation
The implementation shows how the algorithm works with different entries, small or big integer numbers. Another objective is to develop a visual GUI tool that shows how the Shamir secret sharing algorithm can be used. It is easier to demonstrate how the algorithm works with visual and interactive tools.
Conclusion
In summary, this teaching aide empowers you with valuable knowledge about Shamir’s Secret Sharing and its applications in secure data management. By exploring the intricacies of the algorithm, understanding its mathematical foundations, and learning best practices, you will be better equipped to contribute to a secure digital environment.
Let us embark on this journey together—your insights and curiosity are key to a more secure future in cryptography! Thank you for joining us!
You can download the teaching aim here:
Group members:
| Ankita Ankita |
| Oscar Alfredo Constantino Mota |
| Smruti Ranjan Dash |
