On August 13th 2024 NIST published the standards FIPS 203 (Kyber), FIPS 204 (Dilithium) and FIPS 205 (SPHINCS+) which are all quantum resistant algorithms that will soon replace those currently in use. The Kyber standard is a key encapsulation scheme which uses public key enabling and will replace the Diffie Hellman exchange. Dilithium and SPHINCS+ are signature schemes that will replace RSA. Both Kyber and Dilithium use polynomial modular arithmetic that relies on the hardness of a set of problems that can be rephrased as lattice problems which have been proven to be the worst-case quantum hardness – meaning quantum computers can’t solve these problems effectively.
In September 2022 the NSA released a road map on the swap from The Commercial National Security Algorithm Suite(CNSA) 1.0 to CNSA 2.0 which swaps algorithms that are not quantum resistant with the new quantum resistant algorithms.

In this blog I will give a super simplified explanation of Kyber and how it works, based on the Alfred Menezes Cryptography 101 lecture on the subject. I highly recommend watching his lecture if you want to get a better or more in depth understanding. I’ll only be covering Kyber but the Cryptography 101 lecture also covers Dilithium which uses most of the same base mathematical concepts that Kyber uses.
Mathematical Tools used in Kyber
Kyber mainly relies on the mathematical concept of Rq: taking a polynomial of Zq[x] and dividing it by xn+1. Now what does this mean? First q is a prime modulus, and Zq[x] is just a regular polynomial like 3+2x+7x3 but all the coefficients are modulus q. For example, if we instead had a modulus of q=3, our polynomial would change to 2x+x3 as 7 modulus 3 is 1 and 3 modulus 3 is 0. The second part of Rq is dividing by xn+1. This keeps the degree of the polynomial less than n so at most the highest degree of the polynomial is n-1. Kyber uses multiple of these Rq polynomials in matrixes with some linear algebra to perform the algorithm.
Kyber also uses size, which is equal to the absolute value of the highest coefficient in the polynomial. In our example the size of 3+2x+7x3 is 7. Kyber then takes this one step further and uses what’s called a ‘symmetric mod’ instead of a regular modulus. The difference is in the size of the set of integers modulus q: if a number r is greater than (q-1)/2 we take r-q. In practice this means the higher numbers of the modulus are swapped out for negative numbers. See in how mod 17 in figure 2 changes the numbers larger than q/2 to r-q seen in figure 3.
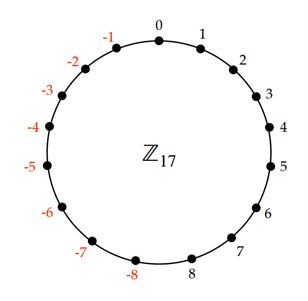
If we again take our example polynomial 3+2x+7x3 but with the symmetric mod 3 (also know as ‘mod-s’ 3) we get -1x+1x3. The modulus of the first equation, 2 mod 3, equals 2 which is larger that q-1/2=1. So we swap it for r-q= 2-3 equaling -1. And remember, the size is the absolute value of the coefficient so if -2 is the largest polynomial coefficient the size is 2.
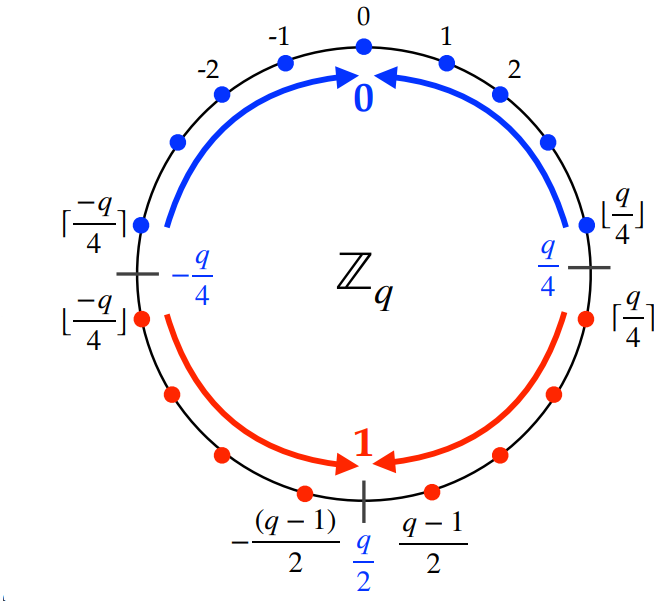
The last base concept Kyber uses is called rounding. This is where we take the result of mod-s q and divide it into two sections. (See figure 4)
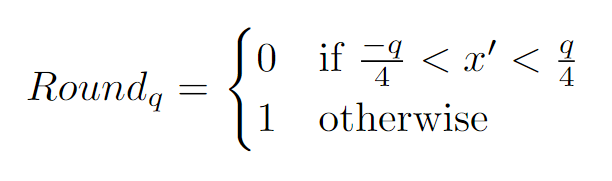
In English, if the result of the mod-s q is on the bottom half of the modulus ring, we round it to a 1 and if its on the top of the modulus ring we round to 0. Well use this to help represent the message we’re sending.
The hard problem that Kyber relies on is called the Decisional Module learning With Errors problem (D-MLWE) which is related to the hardness of the MLWE problem. The MLWE problem goes like this: suppose t = As+e, where each is a matrix of different dimension of Rq polynomials. A is a k by l matrix, t,e and a are all 1 by k. Given t and A, find s. Another important factor is that s and e’s polynomials are a ‘small’ size meaning there bounded by q/2. Having a small size is important as two polynomials with small sizes added together is also relatively small. The addition of e is what makes the problem hard – without it the solution would be relatively simple linear algebra, adding e makes it difficult.
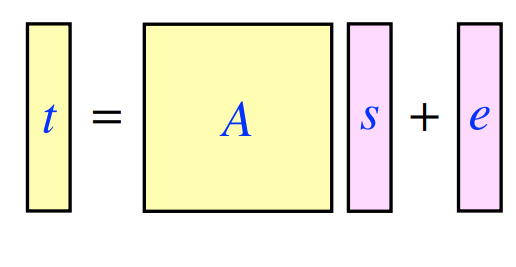
Kyber Protocal
Now for how the protocol actually works: Alice will create an instance of the MLWE problem by choosing t,A,s and e. t and A are Alice’s public key, and s is her private key.
For Bob to encrypt a message m he must first take m in binary [0,1]n and then convert it to a polynomial of n-1th degree where each binary digit is a coefficient i.e 101 becomes 1 + x2. Bob then selects r,e1 and e2 where r is a matrix of Rq with dimensions of 1 by k and the polynomials have size of some small number c1 or less, e1 is the same but with another small size of c2, and e2 is just a singular polynomial of Rq with the same size of c2.
Using these he computes
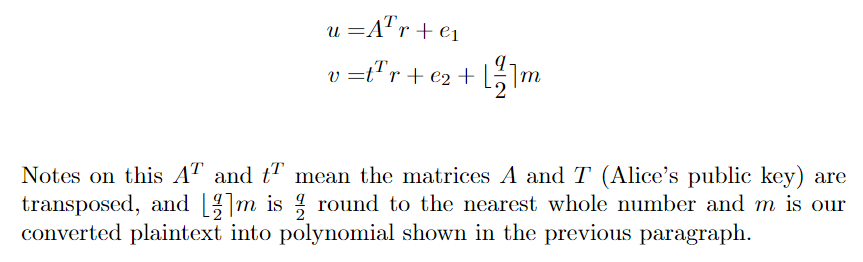
The last thing to note is that all of the Rq polyomials are being randomly generated both for r,e1 and e2 and this is the same for Alice’s A,s, and e. If this seems confusing, following the decryption gives some clarity.
How decryption works: Alice takes u,v and computes Roundq(v-sTu) which will result in the message m. We need to follow the algebra to get a sense why this works.
Alice has v-sTu we can then substitute in the formulas for v and u, giving us
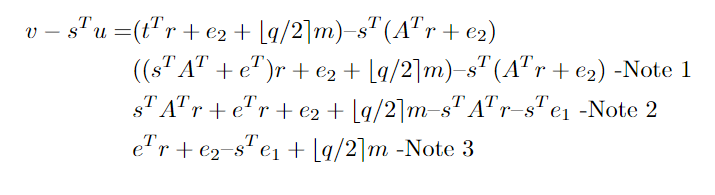
Note 1: Substitute in the formula for t,
Note 2: Expand out the equation
Note 3: Cancel out common term sTATr
Why does this Roundq(eTr+e2 – sTe1 + round(q/2)m) give us back m? Because if the error polynomial eTr+e2 – sTe1 coefficients all round to 0 it’s the same as 0 + round(q/2)m. The error polynomial doing this is not guaranteed, but in practice rounding to 1 happens with such low probability it’s not a concern.
This algorithm allows users to share keys among themselves which would let them then swap to using a symmetric key algorithm like AES. This is a simplified version of Kyber and only goes over the base idea of how it works. Lots of math is simplified and just explained in English – please refer to Alfred Menezes Cryptography 101 lecture to get a more in-depth and mathematical explanation.
With quantum computers getting more and more powerful they are rapidly getting closer to being able to run algorithms that will break RSA and DiffeHellman. As we have learned the ins and outs of these classic algorithms, I believe it is important for us as future cyber security professionals to also be up to date on these new quantum resistant algorithms that will become the standard in the next 5-7 years.
References:
Kyber and Dilithium Cryptography 101 Playlist:
https://www.youtube.com/playlist?list=PLA1qgQLL41SSUOHlq8ADraKKzv47v2yrF
Cryptography 101:
https://cryptography101.ca/kyber-dilithium/
NIST FIPS 203 (Kyber):
https://csrc.nist.gov/pubs/fips/203/ipd
NIST FIPS 204 (Dilithium):
https://csrc.nist.gov/pubs/fips/204/ipd
NIST FIPS 205 (SPHINCS+):
https://csrc.nist.gov/pubs/fips/205/ipd

Good job and interesting topic! With today’s fast advancement in technology and the increased demand for security to keep data confident, integrated, and authenticated. I can say that I pretty much like the effort that NIST puts towards developing and standardizing cryptography algorithms. Introducing Keper as a key encapsulation mechanism (KEM) was a game changer for quantum computers or systems that have the capability to break the old algorithms. But not anymore, as Kyper has complex calculation principles (MLWE, SVP) that addressed and resisted the powerful quantum attacks. What I like most about Kyper is the different key sizes and versions (kyper – 512, kyper – 768, kyper – 1024), which makes it suitable for a wide range of applications. Developers may select between different versions of Kyper based on the level of security needed and the resource constraints.[1][2]
[1] https://cryptopedia.dev/posts/kyber/
[2] https://medium.com/@hwupathum/crystals-kyber-the-key-to-post-quantum-encryption-3154b305e7bd
i want to agree with you that cyber security professionals are meant to be constantly up to date as technology advances on daily basics and so as attacker learn more about the new technology and take advantage of the loop holes and also believe that over time RSA might be broken base on Kyber’s mathematical analysis.
Great post, Hayden! It’s exciting to see that cryptographic researchers are preemptively trying to find new algorithms to replace Diffie-Hellman and RSA, knowing that they are weak to quantum computer. I feel like that perspective contrasts with many businesses’ views on security. Though these algorithms are already being included in standards, I wonder how long corporations will take to implement them. It seems as though many can be slow to change, especially if they don’t have people in the organization who keep up to date on new developments or leadership who understand the importance of cybersecurity.
Thanks for the Comment Nicole, I also have the same thoughts with wondering how long corporations will take to implement these algorithms. I agree that corporations can be slow, but I’d expect them to be faster that you might think. I say this as in the recent years cyber security has been coming more and more into the publics eye and people care more about having privacy and security when they’re on the internet. Already most of the messaging chats are incorporating some form of quantum restraint security into there end to end encryptions. Plus, with the NSA putting out that mandate I mention in the blog I bet once web browser swap over we’ll get wide adoption in the following years quite quickly.
Hayden thanks for the detailed breakdown of how Kyber works and the mathematical tools behind it. The future of cryptography is here, and Kyber seems to be leading the way. I didn’t realize how close we are to transitioning to quantum algorithms like Kyber and Dilithium. It’s reassuring to see the groundwork being laid for a more secure future, especially with quantum computing on the rise.
A very recent informative post! I think this system that was discovered recently is going to be a very advanced model from the perspective of quantum computing data security. Specially using the FIPS 203 (Kyber), FIPS 204 (Dilithium), and FIPS 205 (SPHINCS+) quantum-resistant mechanisms is going to be very tough for the hackers to breach the system. Additionally, the mathematical visualization of Kyber is very tangible. Good work!